Quantization is like compressing a high-resolution image into a smaller file without losing significant visual quality. In computer science and machine learning, it’s a technique used to optimize models and data representation, transforming high-precision formats (e.g., float32) into lower-precision ones (e.g., int8).

This optimization reduces both memory usage and computation costs, making machine learning models more efficient—especially on resource-constrained devices like smartphones or IoT hardware.

This article is the first in a series where we’ll lay the groundwork for understanding quantization. Future articles will dive deeper into inference quantization, post-training quantization, and hands-on implementation examples.

In this introductory piece, we’ll cover:

1. What quantization is and why it matters.

2. How numbers are stored in memory

3. The quantization process: float32 → int8

Let’s get started!

1. What is Quantization and Why Does it Matter?

At its core, quantization is the process of converting data from a high-precision format (e.g., float32) into a lower-precision format (e.g., float16, int8).

This transformation reduces:

• Memory footprint: Smaller data types require less storage.

• Computation costs: Operations on smaller data types are faster and more efficient.

Quantization is especially valuable in machine learning models, where large neural networks need to run efficiently on edge devices like smartphones or IoT systems.

However, quantization isn’t without trade-offs—it often introduces a small amount of accuracy loss. Striking the right balance between efficiency and accuracy is key.

1.1 Types of Quantization

1.1.1 Post-Training Quantization (PTQ)

Post-Training Quantization (PTQ) is one of the most common and straightforward methods for optimizing machine learning models after they have been fully trained. In PTQ, the model is first trained using standard floating-point precision (typically float32) to achieve the desired performance on the training data. Once the training is complete, the model weights and, in some cases, activations are quantized to a lower-precision format (e.g., int8) to improve efficiency during inference.

1.1.2 Quantization-Aware Training (QAT)

Quantization-Aware Training (QAT) is an advanced technique where the effects of quantization are simulated during the training process itself. Unlike Post-Training Quantization (PTQ), which applies quantization after training is complete, QAT integrates quantization directly into the training pipeline. This approach allows the model to learn and adapt to quantization errors, resulting in better accuracy compared to PTQ, especially for models with sharp activation distributions or sensitive layers.

1.2 Quantization of Operators

When applying quantization in machine learning models, it’s not just the data types (float32 → int8) that are adjusted. The operators, which are the mathematical functions (e.g., matrix multiplication, convolution, etc.) performed during inference, must also adapt to the quantized format.

Different strategies exist for quantizing these operators, and each approach comes with specific trade-offs regarding efficiency, accuracy, and hardware compatibility. Let’s explore the three primary types:

1.2.1 Weight-Only Quantization

In Weight-Only Quantization, only the model weights are statically quantized to a lower-precision data type, such as int8. Activations remain in their original floating-point format (float32) during runtime.

1.2.2 Dynamic Quantization

In Dynamic Quantization, the model weights are statically quantized (e.g., during deployment), but activations are dynamically quantized at runtime based on their observed range during inference.

1.2.3 Static Quantization

In Static Quantization, both weights and activations are statically quantized before deployment. This approach requires a calibration dataset to determine the optimal scale and zero-point for both weights and activations.

Now that we’ve explored the primary types of quantization, let’s move on to how these changes affect the mathematical operations within a model. After all, changing the precision of numbers isn’t enough—the functions and calculations performed on those numbers must also adapt to ensure efficiency and accuracy.

2. How Numbers Are Stored in Memory

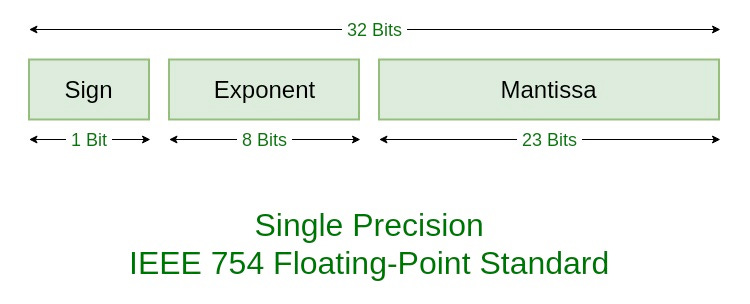
2.1 Floating-Point Representation Recap (float32)

In a 32-bit floating-point representation (IEEE 754 standard), the binary structure is divided into three key components:

1. Sign Bit (1 bit):

   • The first bit determines the sign of the number.

   • A value of ‘0’ indicates a positive number, while a value of ‘1’ indicates a negative number.

2. Exponent (8 bits):

   • The next 8 bits represent the exponent, which defines the scale of the number.

   • The exponent uses a bias of 127 (calculated as $ 2^k-1 $, where k is the number of exponent bits).

   • This bias ensures that both positive and negative exponents can be represented.

3. Mantissa (23 bits):

   • The remaining 23 bits store the significant digits of the number, known as the mantissa or fraction.

   • It includes an implicit leading ‘1’ (for normalized numbers) followed by a fractional binary part that determines the precision of the number.

Example representing the number 0.000000324 in IEEE 754

1. Convert the number to scientific notation: $0.000000324=3.24×10^{-7}$. In binary, this is: \(3.24_{10}​→1.01001110_{2}​ (normalized\space to\space base\space 2)\)
2. Break it into IEEE 754 components:
   • Sign bit: The number is positive, so the sign bit is 0.
   • Exponent: IEEE 754 uses a biased exponent. \(Biased\space exponent=−22+127=105\)
   • Mantissa (fraction): The fractional part $1.01001110_{2}$ is stored without the leading 1 (hidden bit). Only the fractional part 01001110… is stored.
3. Combine the parts for final representation in binary:
   • \[00110100101001110000000000000000\]

This format offers a broad range of values and high precision but is computationally expensive.

2.2 Integer Representation (int32)

Integers are simpler to represent in memory than floating-point numbers. An int32 (32-bit signed integer) uses:

• 1 Sign Bit: 0 for positive, 1 for negative.

• 31 Data Bits: Represent the actual integer value in binary format.

Integers are computationally cheaper to process, making them ideal candidates for quantization.

Key Differences Between Floating-Point and Integer Representation

• Range: Floating-point numbers can represent a vastly wider range of values, including extremely large and extremely small numbers, as well as fractions. Integers, on the other hand, are limited to whole numbers within a fixed range.

• Precision: Integers are exact for whole numbers within their range, while floating-point numbers may introduce rounding errors due to their finite precision and how fractions are approximated.

• Efficiency: Integer operations are generally faster and more computationally efficient than floating-point operations because they require simpler hardware instructions.

Now that we understand how both floating-point and integers are stored, let’s explore how quantization bridges the gap between these two representations.

3. The Quantization Process: float32 → int8

Quantization reduces precision to optimize performance. To convert a float32 number into an int8, we follow these steps:

1. Define a Scale and Zero-Point:

   • Scale: Determines the range of values

   • Zero-Point: Aligns the scale with the target range

   • Apply the Formula: $ q=round(\frac{x-zeropoint}{scale​}) $ ,where
     • q: Quantized value
     • x: Original floating-point value
   • Clamp to the int8 Range: Ensure the result stays between -128 and 127.

Example transformation: float32 → int8

Suppose we have a floating-point number: x = 3.6

• Range: $(-10.0, 10.0)$

• Scale: $\frac{(10 - (-10))}{255} = 0.0784$

• Zero-Point: 0

Using the formula $q=round(\frac{3.6 - 0}{0.0784}​)=46$

So, the float32 value of 3.6 is approximately represented as int8 value 46.

This reduction in precision sacrifices minor accuracy but significantly boosts efficiency.

4. Conclusion

Quantization is a powerful technique that bridges the gap between high-performance machine learning models and the resource constraints of real-world devices. While this process involves trade-offs, such as slight accuracy loss, understanding and applying quantization effectively ensures these compromises are minimized.

In this introductory article, we’ve laid the groundwork by exploring what quantization is, why it matters, and how it bridges the differences between floating-point and integer representations. We’ve also delved into the quantization process, providing a practical overview of the transformation from float32 to int8.

In the next article, we’ll take a closer look at Post-Training Quantization (PTQ). We’ll explore what it is, understand its principles, and walk through coding it from scratch, complete with practical examples to solidify your understanding.

Stay tuned—exciting experiments await!